This chapter builds a foundation of fundamental concepts and definitions that are helpful to fully understanding the geological settings and types of contaminants to which surfactants and cosolvents can be applied. Surfactants and cosolvents are not applicable to all geological settings, nor are they suitable for remediation of all types of subsurface contaminants. It should be recognized that the success or failure of surfactant or cosolvent flushing at a particular site will be determined largely by the degree to which the geology and contaminant distribution are characterized. If the geology and contaminant distribution are not adequately understood, decisions regarding the applicability of surfactant/cosolvent flushing should not be made.
Relevance
This section presents basic concepts that will assist the reader in fully understanding the contaminated subsurface environment. This understanding should, in turn, assist in understanding the application of surfactants and cosolvents discussed in subsequent sections. This section focuses on NAPLs because surfactants and cosolvents are primarily applicable to these types of contaminants. The reader is encouraged to pick and choose the subsections that are of most interest.
Key Concepts
•Moderate- to high-permeability deposits such as sands, gravels, and highly fractured rock lend themselves to the application of chemical flushing technologies, unlike low-permeability deposits such as silts, clays, and sparsely fractured rock.
•Near-surface clay units should be assumed to contain relatively high-permeability features such as fractures, sand seams, root holes, and/or animal burrows, unless proven otherwise.
•LNAPLs and DNAPLs are characterized by their component composition, density, viscosity, and interfacial tension with water.
•Porous media are characterized by their permeability, porosity, dry bulk density, wettability, and displacement pressure.
•NAPL will distribute itself in the subsurface as both disconnected blobs and ganglia of liquid referred to as residual, and in larger accumulations referred to as pools. The amount of NAPL that a porous medium can retain is called the bulk retention capacity.
•NAPLs may give rise to contaminant vapors in the unsaturated zone, as well as dissolved phase plumes below the watertable. The migration of contaminants in these plumes is subject to advection, dispersion, sorption, and degradation (both biotic and abiotic).
•When one fluid displaces another fluid, the displacement process may be hydrodynamically unstable if an unfavorable viscosity and/or density ratio exists between the two fluids. This may impact the successful delivery and recovery of chemical solutions in the subsurface.
The subsurface environment can generally be subdivided into unconsolidated deposits such as sand, gravel, silt, and clay, and consolidated materials such as fractured rock. Unconsolidated materials consisting of gravel and sand can be highly permeable and offer little resistance to the flow of water and contaminants, while those containing a large proportion of silt and clay can be relatively impermeable. The porosity of most unconsolidated materials is typically between 15 and 45 percent.
At most sites, a variety of materials exist, giving rise to heterogeneity. A typical unconsolidated deposit may show a 3 or 4 order-of-magnitude range in permeability at scales as small as centimeters. The degree of heterogeneity will be site-specific and may be the controlling factor in determining the degree to which a delivered chemical mixture can contact contaminated regions of the subsurface. The success, failure, and potential for application of a particular remediation technology typically depends on the degree and type of heterogeneity present in the subsurface.
Until recently, it was thought that most subsurface clay deposits were relatively void of fractures, and therefore provided barriers to contaminant migration. It is currently understood, however, that most near-surface clay deposits contain sparse preferential flow paths regardless of whether they occur above or below the watertable. As an example, fractures in clay can be caused by a variety of mechanisms, including historical desiccation and stress relief. Fractured clay deposits provide a pathway for contaminant migration between overlying and underlying geologic units, and cannot be relied upon to provide a geologic control to vertical contaminant mobilization during remediation efforts.
The depth of contamination at sites may extend down into fractured bedrock, even for overburden thicknesses on the order of 50 m or more. In some cases, no overburden deposits are present and fractured rock is exposed at ground surface. Fractured rock can generally be subdivided into carbonate deposits such as limestone and certain sandstones, which may have a significant matrix porosity; crystalline deposits such as granites, which generally have a low matrix porosity; and volcanic deposits such as interbedded lava flows and cinder beds, which have varyingly high and low matrix porosities. Regardless of the degree of matrix porosity, the primary contaminant migration pathway in fractured rock typically is the fracture network. Because the volume of open void space in the fracture network is small, even small volumes of contaminants can migrate substantial distances in fractured rock. It is important to note that, typically, only a minority of the open fractures represent the majority of flow pathways in rock. This presents a challenge in attempting to contact all contaminated regions of the rock mass with injected remedial agents such as surfactants and cosolvents.
In general, deposits containing appreciable amounts of low-permeability material, such as silt and clay, and some fractured bedrock deposits do not lend themselves to the application of surfactants and cosolvents. These geological settings are not suitable for chemical flushing because of the large amount of time that will be required to pass a specified volume of fluid through the contaminated zone. Surfactant and cosolvent flushing are more suited to moderate- and high-permeability deposits where large volumes of fluid can be flushed through the target zone in a reasonable amount of time. The degree of contaminant removal that will occur during a surfactant/cosolvent flood will, in general, be higher for deposits showing less heterogeneity.
Subsurface contaminants can be grouped into various classes, including synthetic organic compounds, naturally occurring organic compounds, metals, cations, anions, micro-organisms, and radionuclides. Synthetic organic compounds are the focus of this manual because they lend themselves to removal using surfactant/cosolvent flushing. Most synthetic organic compounds encountered at contaminated sites are only sparingly soluble in water. As a result, they can exist in the subsurface as a separate liquid phase, often referred to as a nonaqueous phase liquid (NAPL).
Organic liquids that are heavier than water are referred to as dense, nonaqueous phase liquids (DNAPLs). Examples of such liquids include chlorinated solvents, PCB oils, creosote, and coal tar. Because they are more dense than water, DNAPLs have the potential to migrate to great depths below the watertable. Organic liquids that are lighter than water are referred to as light, nonaqueous phase liquids (LNAPLs). Examples of LNAPLs include gasoline, jet fuel, and heating oils. LNAPLs tend to accumulate above and slightly below the watertable.
In a contaminant hydrogeology context, phases are defined according to their fluid-mechanical properties. Examples of phases include water, air, LNAPL, and DNAPL. Phases do not mix freely with each other and therefore exist in the subsurface as separate fluids characterized by their own density and viscosity. Strictly speaking, materials such as aquifer solids and rock are also classified as phases. Components, on the other hand, are the individual chemical species that comprise the phases. Any phase can be composed of any number of components. In some cases, the DNAPL of concern at a site will be a single-component DNAPL, while in other cases 70 or 80 components may be present. Gasoline is an example of an LNAPL containing more than 200 individual components. Dry-cleaning fluid is a DNAPL containing only one component (tetrachloroethylene, or PCE).
Multiphase/multicomponent flow and transport therefore refers to the migration of fluid phases through either fractured or porous media and the simultaneous migration of any number of components within any of the phases. Components are also able to partition across phase boundaries, giving rise, for example, to the formation of contaminant vapors in unsaturated media and aqueous phase plumes below the watertable. It is important to measure the component composition of NAPL encountered at a hazardous waste site as part of the remedial design because the effectiveness of a particular type of surfactant or cosolvent may be highly dependent on the chemical composition of the NAPL at hand.
The density of a liquid is defined as its mass per unit volume. The density of water is 1000 kg/m3 at 4°C. Most LNAPL compounds of concern at sites have densities ranging from 700 kg/m3 to 900 kg/m3. Most DNAPLs encountered at sites have densities ranging from 1030 kg/m3 to 1700 kg/m3. If the NAPL of concern is a single-component NAPL, then its density can be estimated using a textbook value. However, the density of a multi-component NAPL will likely not be listed in a handbook and will need to be measured using a sample of recovered liquid. Density is a weak function of temperature for the range of temperatures usually encountered in the subsurface. Most NAPLs exhibit a slight increase in density with decrease in temperature. Examples of handbooks listing the density of organic compounds typically encountered at hazardous waste sites include Verschueren (1983) and Mackay, et al. (1993).
At a contaminated site, DNAPLs and LNAPLs may be composed of several
components. It will be possible, for example, to find lighter-than-water
compounds, such as toluene and xylene, as part of a DNAPL phase. Conversely,
heavier-than-water components such as chlorinated solvents may be part of a
LNAPL. The overall density of the NAPL will depend on the relative proportions
of lighter- and heavier-than-water components. Table 3-1 presents the component
composition of DNAPL found at the S-Area site in New York State (Cohen and
Mercer, 1993). As can be seen, this DNAPL contains a small amount of toluene,
which in its pure form is an LNAPL. The DNAPL also contains some components
that are solids in their pure form. Because the majority of components are
liquids more dense than water, however, a DNAPL phase exists. The implication
is that it is possible to detect lighter-than-water components such as toluene
far below the watertable without the presence of an actual LNAPL source in the
subsurface. It is also clear that the density and viscosity of NAPLs will be
site-specific because these properties depend upon component composition.
| Table 3-1 | |||||
| Component Composition of S-Area DNAPL | |||||
Compound |
Single Component Density (kg/m3) |
||||
|---|---|---|---|---|---|
| Chlorobenzene | 1107 | 0.8 | |||
| Dichlorobenzene | 1305 | 0.6 | |||
| Trichlorobenzene | 1574 | 11.5 | |||
| Tetrachlorobenzene | 1858 | 32.0 | |||
| Pentachlorobenzene | 1609 | 6.4 | |||
| Hexachlorobenzene | 2044 | 1.6 | |||
| Toluene | 867 | 0.1 | |||
| Chlorotoluene | 1082 | 0.9 | |||
| Dichlorotoluene | - |
0.9 | |||
| Total BHCs | 1870 | 0.4 | |||
| Carbon Tetrachloride | 1590 | 1.0 | |||
| Trichloroethylene | 1460 | 0.4 | |||
| Tetrachloroethylene | 1626 | 13.0 | |||
| Hexachloroethane | 2090 | 1.1 | |||
| Hexachlorobutadiene | 1675 | 4.2 | |||
| Hexachlorocyclopentadiene | - |
12.0 | |||
| Octachlorocyclopentadiene | - |
14.0 | |||
| Mirex | Solid | 0.1 | |||
| Edosulfan II | Solid | 0.3 | |||
Source: Cohen and Mercer, 1993. |
|||||
The density of a NAPL is an important design parameter when considering the use of surfactants and cosolvents. Even if the NAPL of interest is more dense than water, its properties may prevent it from migrating downward through certain geological layers. When introducing a surfactant or cosolvent, the NAPL properties may change such that the NAPL can now migrate downward into previously uncontaminated regions. This is referred to as vertical mobilization of NAPL. At some sites, one primary remedial design objective may be to select a surfactant/cosolvent system that minimizes the propensity for vertical NAPL remobilization.
The viscosity of a liquid is a measure of its resistance to fluid flow. The viscosity of water ranges from 0.0015 Pa.s at 5°C to 0.0010 Pa.s at 20°C (Streeter and Wylie, 1981). Certain NAPLs, such as some chlorinated solvents, are characterized by viscosities less than that of water, implying that they are highly mobile in the subsurface. Other NAPLs, such as coal tar, are significantly more viscous than water. Viscosity is very dependent on temperature and should always be evaluated at the temperature of interest. As with density, the viscosity of a single-component NAPL can be obtained from a handbook (e.g., Verschueren, 1983). The viscosity of a multicomponent NAPL, however, will be site-specific and should be measured from a recovered sample.
The viscosity of a NAPL is an important parameter to measure when pumping and mobilization of NAPL is to take place at a site. Faster rates of recovery can be expected for low-viscosity NAPLs compared to high-viscosity NAPLs, all other factors being equal. In addition, the likelihood of forming an unstable and uneven displacement front in which some of the NAPL is bypassed and penetrated by "fingers" of the delivered chemical solution is partially dependent on the ratio of NAPL to injected fluid viscosity. In an unstable surfactant or cosolvent displacement process, it is very unlikely that a significant amount of contaminant removal will take place.
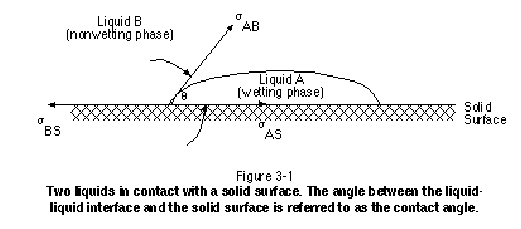
Wettability refers to the affinity of one immiscible fluid for a solid surface in the presence of a second or third immiscible fluid. Figure 3-1 illustrates a drop of liquid "A" resting on a solid surface in the presence of liquid "B." As shown, the liquid-liquid interface meets the solid surface at a specific angle that is referred to as the contact angle. The fluid through which this angle is measured to be less than 90 degrees is referred to as the wetting phase. The other fluid, through which the angle is measured to be greater than 90 degrees, is referred to as the nonwetting phase. In the event that one phase spontaneously spreads to coat the entire solid surface, the contact angle is zero and that phase is referred to as being perfectly wetting. In such cases, the nonwetting phase does not physically touch the solid surface, but is separated from the solid surface by a thin layer of the wetting phase. If the contact angle is between 70 and 110 degrees, the system is said to exhibit intermediate wettability.
The contact angle that exists between a NAPL and water in a given geologic setting depends not only on the individual components that comprise the NAPL and the water, but also on the surface chemistry of the solid in question. Wettability is therefore site-specific and may even vary within a particular site, in which case the site is said to exhibit mixed wettability. A reliable method of establishing whether a NAPL is wetting or nonwetting at a site is to measure a capillary pressure-saturation curve using the NAPL, porous medium, and other fluid in question.
For most contaminated sites, NAPL can be assumed to be nonwetting with respect to water provided that the aquifer solids contain little organic matter. A peat bog, however, is an example of a site where NAPL may be wetting with respect to water. Above the water-table, it is usually appropriate to assume that water is wetting with respect to NAPL and that NAPL is wetting with respect to air. Extra care should be taken, however, when dealing with coal tar or creosote sites. These NAPLs are typically complex mixtures that may contain a significant portion of highly insoluble and possibly polymerized pitch. This pitch may be reactive and has the potential to significantly alter the wettability of aquifer solids. For coal tar and creosote sites, wettability should be measured and not assumed. Lake (1989) discusses the influence of wettability on relative permeability, capillary pressure, electrical properties, and waterflooding.
Interfacial tension refers to the tensile force that exists in the interface separating two immiscible fluids (e.g., phases). This force arises due to a mutual attraction between molecules in the vicinity of the interface and like molecules in bulk solution. This also can be thought of as a mutual dislike for molecules on the opposite side of the interface. Interfacial tension results in the interface between immiscible liquids taking on a shape of minimum area. If there were no interfacial tension between water and the liquids of concern, they would be termed aqueous phase liquids rather than nonaqueous phase liquids. In other words, they would be fully miscible with water.
For many laboratory-grade organic compounds, such as chlorinated solvents, the interfacial tension with water is on the order of 0.040 to 0.050 N/m (note that 1 N/m=1000 dynes/cm). As a comparison, the interfacial tension between pure water and air (often referred to as surface tension) is approximately 0.072 N/m. At industrial waste sites, the interfacial tension between NAPL and water is typically between 0.005 and 0.035 N/m, depending on the specific components that comprise both the NAPL and the water. If some of the components act as surface active agents (surfactants), the interfacial tension will tend to be toward the lower end of this range, and possibly even less. Examples of such surfactants include additives in various fuels and cleaners. Interfacial tension is therefore a site-specific parameter that must be measured on an actual sample of NAPL obtained from the subsurface. It is important to note that the application of a surfactant or cosolvent flood will usually result in a lowering of NAPL-water interfacial tension (Fountain, et al., 1991).
Capillary pressure refers to the pressure discontinuity that exists across a curved interface separating two immiscible fluids. This pressure difference exists because of the interfacial tension present in the fluid-fluid interface separating the two fluids. The capillary pressure (Pc) is defined as the nonwetting phase pressure (Pnw) minus the wetting phase pressure (Pw). For an arbitrarily shaped interface, the capillary pressure is represented by the following equation:
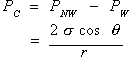(1)
where
is the interfacial tension, 
is the contact angle, and r is the mean radius of
curvature (which is a function of the pore throat size). Equation (1) shows
that the pressure drop across the interface is directly proportional to the
interfacial tension and inversely proportional to the radius of curvature. It
follows that higher capillary pressures are required for the nonwetting phase
to enter finer grained materials. As a result, NAPL migration below the
watertable is typically confined to the relatively coarser grained lenses and
laminations. This is illustrated clearly in the work of Kueper, et al. (1989).
In a two-phase system such as DNAPL and water below the watertable, the nonwetting phase will always be present on the concave side of the interface separating the liquids in question. The wetting phase will be present on the convex side of the interface and will preferentially reside in the smaller pores and pore throats. This microscopic-scale distribution of fluids is illustrated schematically in Figure 3-2. It is assumed in this figure that DNAPL is the nonwetting phase and that water is perfectly wetting on the grain surfaces. Note that DNAPL does not occupy all of the pores in the figure and that water can therefore flow past the DNAPL-water interfaces, thereby allowing contact with injected agents such as surfactants and cosolvents.
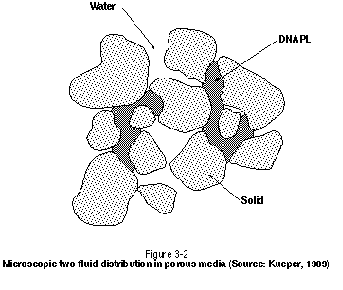
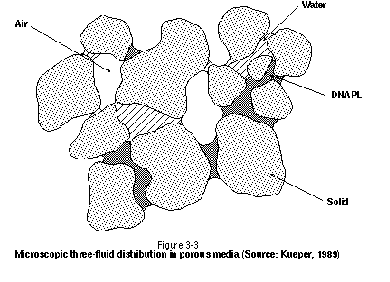
Figure 3-3 presents a similar pore-scale distribution of fluids for a three-phase system in unsaturated porous media. The DNAPL- air interfaces are drawn concave toward the air because DNAPL is wetting with respect to air, while the DNAPL water interfaces are drawn concave toward the DNAPL because water is wetting with respect to DNAPL. Note that components can partition across DNAPL-water interfaces (DNAPL dissolution), DNAPL-air interfaces (vaporization), and water-air interfaces (volatilization). In addition, any components present in the water phase may partition to the grain surfaces (sorption).
In the majority of cases, it is not possible to define the pore-scale geometry of a geological material such that the positions of individual fluid interfaces can be calculated. If this were possible, however, the relationship between capillary pressure and fluid saturation could be established. As an alternative, it is customary to represent the relationship between capillary pressure and fluid saturation by means of a capillary pressure-saturation curve measured at the macroscopic scale. The macroscopic scale represents an average over many pores and pore throats.
Figure 3-4 presents a typical capillary pressure-saturation curve for a two-phase system in porous media. A similar curve would apply to a two-phase system in a rough-walled fracture (Reitsma and Kueper, 1994). The wetting and nonwetting phase saturations are expressed as an average percentage of pore space. It is important to note that the capillary pressure-saturation relationship is hysteric. As can be seen in Figure 3-4, a higher degree of nonwetting saturation can be attained only with higher capillary pressures. This corresponds to the fact that progressively smaller pores and pore throats will be invaded at higher capillary pressures. The threshold capillary pressure required to invade an initially wetting-phase-saturated porous medium is referred to as the displacement pressure. In general, deposits from below the watertable that are void of root holes and worm holes will exhibit a more distinct displacement pressure than materials from above the watertable.
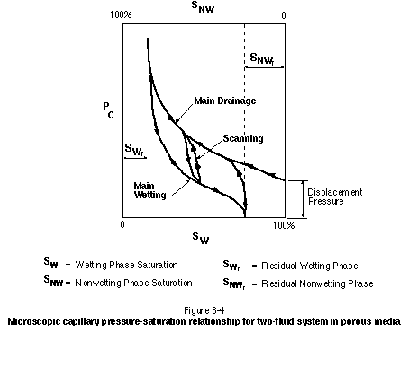
The shape of the capillary pressure-saturation curve depends on many factors, including grain sorting, contact angle, interfacial tension, and hydraulic conductivity. Of greatest practical interest at a site is the variation of the capillary pressure-saturation relationship with hydraulic conductivity. In general, a lower hydraulic conductivity material or a smaller aperture fracture will exhibit a higher displacement pressure. This is illustrated in Figure 3-5 for a suite of PCE-water capillary pressure curves measured by Kueper and Frind (1991) from samples of sand obtained from the Borden aquifer in Canada. Note that the lower permeability samples exhibit a vertically higher capillary pressure curve. The Borden aquifer is relatively homogeneous with respect to hydraulic conductivity. A suite of capillary pressure curves for an aquifer containing a wider range of materials (e.g., silt through gravel) would exhibit a wider range of displacement pressures than those shown in Figure 3-5.
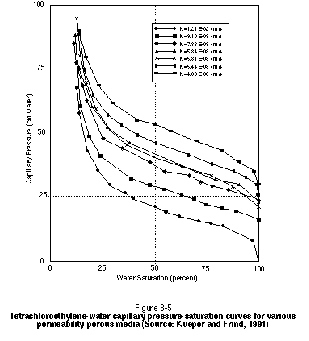
Establishing the capillary characteristics of an aquifer (e.g., the displacement pressure) is an important step in designing a surfactant or cosolvent flood. If a strong capillary barrier (such as unfractured clay) exists beneath the targeted zone of contamination, for example, vertical mobilization of DNAPL may not be of concern. On the other hand, if the primary objective of the chemical flood is to mobilize NAPL, then sufficient interfacial tension reduction must be brought about to sustain NAPL migration through regions exhibiting high capillary resistance.
Residual NAPL refers to the presence of small, disconnected blobs and ganglia of organic liquid that are trapped in the pore spaces of porous media or fractures by capillary forces. Residual NAPL is formed at the trailing end of a migrating NAPL body by snap-off and by-passing mechanisms. In porous media, blobs of residual NAPL are typically between 1 and 10 pore throats in length. It is currently understood that NAPL migration cannot take place through the subsurface without the formation of residual NAPL.
In the unsaturated zone, components will partition from residual NAPL to the air phase, giving rise to vapor plumes, and from residual NAPL to soil moisture and infiltrating water, giving rise to aqueous phase contamination. Below the watertable, residual NAPL will dissolve into flowing groundwater, resulting in dissolved contaminant plumes.
The degree of residual NAPL formed in a particular medium is a function of many factors, including NAPL density, NAPL viscosity, interfacial tension, medium permeability, and the maximum capillary pressure attained during the original migration process. In general, residual NAPL saturations will vary from between 2 percent and 30 percent of pore space (approximately 1 to 10 percent of bulk volume) and will be spatially variable at a site. It must be noted, however, that this saturation refers to the amount of NAPL actually present in the lenses, laminations, or fractures invaded by the migrating NAPL. As will be discussed further below, the concept of bulk retention capacity is more useful for estimating the volume of NAPL retained in the subsurface at real sites.
Pooled NAPL refers to the presence of NAPL at saturations higher than residual. Pooled NAPL is distinctly different than residual NAPL in that pooled NAPL represents a continuous fluid distribution and is potentially mobile in the subsurface. While the relative permeability assigned to residual NAPL is zero, pooled NAPL has a finite relative permeability determined by the degree of saturation present. In general, pools contain NAPL saturations of between 30 percent and 80 percent of pore space.
NAPL pools tend to form above capillary barriers. Below the watertable, with DNAPL being nonwetting with respect to water, DNAPL would pool on fine-grained lenses. LNAPL would tend to pool on high-water-content layers in the unsaturated zone. Significant pooling of LNAPL also may occur in the vicinity of the watertable. Because of the heterogeneous nature of subsurface deposits, NAPL pools can form at all elevations and not necessarily just on major - permeability units such as clay aquitards and bedrock surfaces.
The presence of pooled NAPL can be problematic at sites because drilling through NAPL pools can lead to vertical short-circuiting. NAPL pools also can be mobilized in response to groundwater pumping, which can be an advantage if extraction wells are properly placed, but a disadvantage if mobilization occurs into previously uncontaminated regions of the subsurface. NAPL pools also can be mobilized if injected agents such as surfactants and cosolvents lower the NAPL-water interfacial tension. For the case of DNAPL below the watertable, the height of pooled DNAPL can be calculated by considering a force balance in a one-dimensional, hydrostatic system (Kueper, et al., 1993):
(2)
where H is the height of connected-phase DNAPL,
Pc" is the capillary pressure at the base of the pool,
Pc' is the capillary pressure at the top of the pool, Dr is
the difference in density between the DNAPL and water, and g is the
acceleration due to gravity. The maximum pool height that can be supported
above a given capillary barrier is calculated by substituting the barrier
displacement pressure, Pd, for 
in
Equation (2). Because a lowering of interfacial tension will decrease the
displacement pressure of a given porous medium, it can be seen from Equation
(2) that the application of a surfactant or cosolvent flood has the potential
to cause vertical pool mobilization.
The bulk retention capacity of a porous or fractured medium is defined as the volume of NAPL divided by the overall volume of medium within which the NAPL migration pathways occurred. This overall volume includes the total volume of soil, gas, and liquid through which the NAPL has migrated. In other words, this overall volume of medium includes both those lenses and laminations in which residual and pooled NAPL is present and the adjacent lenses and laminations void of NAPL. The concept of bulk retention capacity is particularly useful at real sites where it is virtually impossible to detect each individual lens and lamination containing residual and pooled NAPL.
The bulk retention capacity is dependent upon several factors, including the nature of the release (e.g., slow dripping versus catastrophic spill), interfacial tension, and the bedding structure of the medium. The bulk retention capacity of natural field deposits generally will be much less than laboratory-derived values because of the heterogeneous nature of field deposits. For typical silt, sand, and gravel deposits exhibiting structure, DNAPL bulk retention capacities are expected to range between 0.25 percent and 3 percent by bulk volume, with the lower values in this range applicable to more heterogeneous deposits not having laterally extensive capillary barriers. This range of bulk retention capacities is based on a variety of field experiments involving the release of DNAPL into a natural sand aquifer (Kueper, et al., 1993; Poulsen and Kueper, 1992; Brewster, et al., 1995).
Figure 3-6 illustrates the concept of bulk retention capacity. The figure shows a release of DNAPL into a horizontally bedded aquifer. The overall volume into which DNAPL was released is an upright cone with a height of 10 m and a base width of 10 m. Using a bulk retention capacity of 2 percent, the volume of residual and pooled DNAPL inside the cone is approximately 5.2 m3. It should be noted that exceptions will occur where the use of bulk retention capacities between 0.25 percent and 3 percent may not be appropriate. One example involves the presence of a significant pool of LNAPL in the vicinity of the watertable in a shallow aquifer. In this case, the bulk retention capacity may be much higher than 3 percent because of the dominating influence of the watertable.
The conductance of fluid flow that a porous or fractured medium exhibits is referred to as its permeability. This is also often thought of as the resistance to fluid flow. Finer-grained materials exhibit lower permeabilities while coarser-grained materials generally exhibit higher permeabilities. Permeability is a function of the medium only, not the fluids present in the medium. For a medium saturated with water, it is customary to define the term hydraulic conductivity. Unlike permeability, hydraulic conductivity takes into account the particular fluid that is present in the medium. In an isotropic medium, hydraulic conductivity is defined as:
(3)
where K is the hydraulic conductivity, k is the permeability, r is the fluid density, g is the acceleration due to gravity, and m is the fluid viscosity. It is clear from Equation (3) that Kincorporates both medium (k) and fluid (r,m) properties.
When the pore space of a porous or fractured medium is occupied by two or more fluids, the permeability of the medium to any one of the fluids is reduced. The presence of a second or third fluid reduces the number of pores and pore throats available for flow and increases the tortuosity of available flow paths. To account for the reduction in permeability due to the presence of additional fluids, a relative permeability can be defined as follows:
(4)
where kr is the relative permeability of the fluid of interest and keff is the effective permeability of the fluid of interest.
If only one fluid occupies the medium of interest, the effective permeability would equal the permeability and the relative permeability to that one fluid would be 1. As increasing amounts of a second or third fluid occupy the medium, the relative permeability to the first fluid would decrease. Numerous studies in the published literature have demonstrated that relative permeability is a function of fluid saturation (Bear, 1972; Corey, 1986). Figure 3-7 presents the typical relationship between relative permeability and fluid saturation in a two-phase system. It is clear that as the relative permeability to one phase increases, the relative permeability to the other phase decreases. Although relative permeability curves for a two-phase system generally follow the trends exhibited in Figure 3-7, the specific shapes of the curves are a function of many factors, including interfacial tension and medium structure.
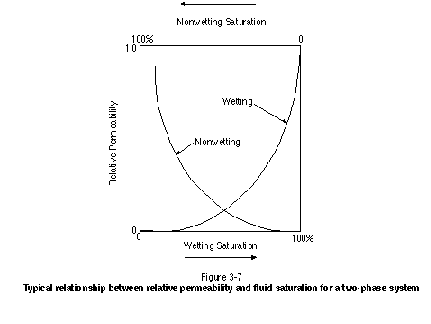
Relative permeability curves are required to calculate the fluid flux for a multiphase system. For a single-phase system, Darcy's Law can be used to calculate the fluid flux as follows:
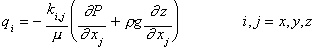(5)
where is the flux in the i direction,
is the permeability tensor, and 
is the fluid pressure.
For a system where more than one fluid phase is present, Equation (5) is written for each phase and is modified by incorporating the relative permeability function as follows:
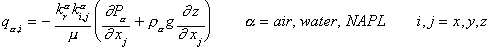(6)
where 
is the relative permeability of
the a phase.
In practice, the following form of Darcy's Law is often used to calculate the flux of groundwater in a steady-state, single-phase flow system:
(7)
where qi is the groundwater flux in the i direction,
Kijis the hydraulic conductivity tensor,
is the average hydraulic gradient, and
h is the hydraulic head defined as:
(8)
where y is the pressure head and z is the elevation head. The spatial and temporal distribution of the hydraulic head can be mapped easily at sites by measuring the water level in piezometers. The difference in water level between two piezometers ( h), divided by the distance between the piezometers ( L), can be used to estimate the hydraulic gradient (Ñh) between the two points. The average linear groundwater velocity is obtained from the flux as follows:
(9)
where is the velocity in the i direction and f is the medium porosity.
It should be noted that Darcy's Law is valid for steady-state, laminar fluid flow. At a site where fluid flow is transient, the partial differential equation describing fluid flow must be solved. Transient flow will occur in response to events such as groundwater pumping and infiltration of rainwater or snow melt. There are several commercially available groundwater flow models suitable for simulating transient, single-phase flow in a wide range of geological environments. Simulating the flow of multiple fluids, such as LNAPL or DNAPL migration in groundwater, requires the use of a multiphase flow model. A multiphase flow model, however, is considerably more challenging to use than a groundwater flow model. Some of the difficulties associated with parameter estimation and output uncertainty in multiphase flow modeling are discussed by Kueper and Frind (1996) and in Section 5.4 of this manual.
For most surfactant and cosolvent applications, it is useful to define the concept of a pore volume and the time required to pass one pore volume of solution through a zone of interest. A pore volume refers to the volume of water in a region of interest. For a rectangular region of aquifer, one pore volume would be the volume of this rectangle multiplied by the aquifer porosity. Assuming one -dimensional, steady-state groundwater flow, the time required to pass one pore volume of solution through a region of interest can be calculated as:
(10)
where tp is the time required to pass one pore volume, 
is the average linear groundwater velocity, and x is
the length of the region of interest in the direction of groundwater flow. For
transient flow systems and irregular geometry, a commercially available
groundwater flow model can be employed to calculate the time for passing one
pore volume.
As an example, consider a fine- to medium-grained sand aquifer with a porosity of 35 percent and a hydraulic conductivity of 5 × 10-3 cm/s. An injection-withdrawal system is to be installed by placing a row of closely spaced injection wells 20 m from a row of closely spaced withdrawal wells. This configuration of wells results in approximate steady-state, one-dimensional groundwater flow. The injection and withdrawal rates are set to achieve an average hydraulic gradient of 0.05. Equation (7) shows that the flux through the system is 2.5 × 10-6 m/s. Equation (9) shows that the average linear groundwater velocity is 7.14 × 10-6 m/s . Equation (10) shows that the time for one pore volume to pass is 32.4 days. It follows that a surfactant or cosolvent flood requiring 10 pore volumes of flushing, for example, would require 0.9 years of operation. This is discussed further in Section 5.1.5.
In general, a less viscous fluid displacing a more viscous fluid will result in viscous fingering. Viscous fingering can result in substantial portions of the subsurface not being contacted by the injected solution. Because most surfactants and cosolvents of interest are more viscous than water, viscous fingering will be of concern at the back end of an injected surfactant/cosolvent slug that is being pushed by water injection.
Similar to viscous fingering, a less dense fluid displacing a more dense fluid upwards is subject to gravitational instability. Elongated fingers of the less dense fluid will project up into the more dense fluid, by-passing certain regions of the subsurface. In cases where either the viscosity or density ratio is favorable, and the other is unfavorable, a threshold velocity exists beyond which the system will be stable. Further discussion of fingering is provided by Kueper and Frind (1988). The use of polymers and foams to combat the formation of unstable displacements is discussed in a subsequent section addressing sweep efficiency.
The transfer of components from the NAPL phase directly to the air phase is referred to as vaporization. Vaporization will lead to the formation of contaminant vapors in unsaturated media. These vapors can advect and disperse through the continuous air pathways present in unsaturated media, thereby spreading contamination beyond the immediate area of the NAPL. The rate of vaporization and magnitude of air-phase concentrations is proportional to a compound's vapor pressure (the pressure exerted in the air phase above the pure compound in a closed container), which is a strong function of temperature. Vapor pressure typically increases with higher temperatures.
Certain NAPLs, such as trichloroethylene (TCE), have a significant vapor pressure and can therefore give rise to large vapor plumes. Vaporized contaminants may diffuse into soil moisture, up through the ground surface, down to the watertable, and into infiltrating water. The vapor pressure and resulting maximum air phase concentrations for typical NAPLs can be found in handbooks such as Verschueren (1983) and Mackay, et al. (1993). For a multicomponent NAPL, a compound's effective vapor pressure should be calculated. For structurally similar compounds, the use of Raoult's Law, which stipulates that the effective vapor pressure of the component in question will equal the product of its single-component vapor pressure and its mole fraction in the NAPL phase, has been found to be appropriate for calculating vapor pressures in a multicomponent system. The behavior of contaminant vapors in unsaturated media is discussed further by Mendoza, et al. (1996).
The partitioning of components from the water phase to the air phase is referred to as volatilization. The magnitude of concentrations arising from volatilization is described by Henry's Constant, which is defined as the equilibrium concentration in the air phase divided by the equilibrium concentration in water. A high Henry's Constant indicates a high affinity for the air phase. Care should be taken when using a Henry's Constant in calculations because various units can be used to define this parameter in handbooks. It should also be noted that if groundwater contains dissolved compounds at their aqueous solubility, the same air phase concentration will arise from the volatilization process as from the vaporization process. The Henry's Constant for typical organic contaminants encountered at hazardous waste sites can be found in handbooks such as Verschueren (1983).
The partitioning of components from the water phase to solid matter such as sand grains and fracture walls is referred to as sorption. Sorption can be classified as adsorption, which refers to the partitioning of components to the actual surface of solid matter, and absorption, which refers to the diffusion of components into the pore space within soil grains. Having diffused into a grain or other solid particle, components may also adsorb to the interior surfaces of these particles. For typical organic contaminants, the degree of adsorption is a function of both the type of organic compound and the degree of organic carbon present on the solid surfaces.
At sites where sorption is occurring, the leading edge of the contaminant plume will migrate at a slower rate than the groundwater. This process is commonly referred to as retardation. The ratio of groundwater velocity to contaminant velocity can be characterized by the retardation factor:
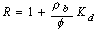
(11)
where R is the retardation factor, rb is the dry bulk density of
the medium, f is the medium porosity, Kd is the distribution
coefficient,
is the average linear groundwater velocity, and
vcis the contaminant velocity. Equation (11) assumes an equilibrium
sorption process. Modifications need to be made in cases where the sorption
process is rate limited. Fetter (1993) presents an introductory discussion of
nonequilibrium sorption.
The distribution coefficient, Kd, is often approximated as:
(12)
where KOC is the organic carbon partition coefficient and fOC is the fraction organic carbonpresent on the solid matter. KOC can be estimated using empirical relationships that are a function of either KOW, the octanol-water partition coefficient, or the aqueous solubility of the compound of interest (Fetter, 1993). These estimation methods are subject to a certain degree of uncertainty. If accurate definitions of Kd or R are required, laboratory batch tests, column tests, and pilot field tests should be considered.
It is clear that the degree of retardation experienced by a particular contaminant is a function of both the medium through which solute transport is occurring and the nature of the particular contaminant. Retardation factors will therefore be site-specific. The presence of cosolvents such as alcohols in groundwater also will influence the sorption process. The influence of alcohols on desorption and the sorption of surfactants is discussed in later sections.
Relevance
This section uses the basic concepts presented above to describe the migration and distribution of contaminants in the subsurface. This information is important in understanding the physical setting in which surfactants and cosolvents may be applied. Readers with extensive experience investigating sites contaminated by both LNAPLs and DNAPLs may choose to skip this section.
Key Concepts
•LNAPL and DNAPL migration through unconsolidated deposits such as sands, silts, and gravels is influenced primarily by geological structure.
•Lateral flow and pooling of DNAPL can occur in response to even subtle variations in permeability and geological structure.
•Finding individual DNAPL pools and zones of residual at a site often is not practicable. Remediation efforts need to be applied over larger volumes of the subsurface within which pools and zones of residual exist.
•Although it is commonly thought that LNAPL "floats" on the watertable, this is incorrect. Significant portions of LNAPL may have been carried below the watertable during the initial migration process and in response to watertable fluctuations.
•The time required for NAPL to fully dissolve into groundwater is typically on the order of a few decades to a century or longer.
•Because the bulk retention capacity of fractured media is low, even small volumes of NAPL can migrate significant lateral and vertical distances in fractured rock and clay.
•In fractured media with a significant matrix porosity, substantial amounts of contaminant can diffuse into the matrix. The time required for contaminants to diffuse back out of the matrix can be on the order of several decades.
Following release at the ground surface, a NAPL will migrate down through the unsaturated zone, distributing itself both as residual and in pools. Because NAPLs are typically wetting with respect to air and nonwetting with respect to water, they will imbibe into dry, finer-grained layers and will flow laterally along any high-water-content layers not exhibiting continuous air pathways. NAPL in the unsaturated zone will therefore typically exist at negative pressure and will not flow into an open borehole or excavation.
NAPL migration through unsaturated porous media is extremely sensitive to bedding structure as a result of capillary forces. The color photographs presented in Poulsen and Kueper (1992) show the migration pathways of DNAPL (PCE) in the unsaturated zone of a sandy aquifer located at Canadian Forces Base Borden. In this study, DNAPL was found to migrate distinctly through certain lenses and laminations and not through others. DNAPL migration was governed by geologic structure, with migration pathways always following the strike and dip of individual lenses and laminations. At times, the lenses and laminations through which DNAPL migration occurred were no more than a few millimeters in thickness. It was found that the variation in hydraulic conductivity between adjacent laminations and lenses was generally less than a factor of two. This subtle variation in hydraulic conductivity at the millimeter to centimeter scale, although sufficient to govern DNAPL migration, would be virtually impossible to characterize at contaminated sites using present-day hydrogeological investigation methods.
Once present in unsaturated media, residual and pooled NAPL may vaporize, giving rise to vapor plumes. In dry and warm environments, vaporization may deplete all residual and pooled NAPL in as short as a few years, depending on the vapor pressure of the particular NAPL. In such cases, however, the vapor phase, aqueous phase, and sorbed phase contamination may persist for several decades or longer.
LNAPL migration through the unsaturated zone will be similar to DNAPL migration, except in the vicinity of the watertable. Because LNAPL is less dense than water, significant pooling can occur. It is important to note, however, that LNAPL does not "float" on the watertable. Detailed examination of the distribution of LNAPL in the vicinity of the watertable will show that the lower portion of the LNAPL pool is at positive pressure and exists below the watertable. At some location in the LNAPL pool, the LNAPL table exists, with LNAPL at negative pressure above this surface. Only LNAPL at positive pressure is recoverable using skimmer pumps in monitoring wells. The LNAPL at negative pressure, although representing a continuous and potentially mobile phase, will not flow into an open borehole or monitoring well. Figure 3-8 presents a general schematic illustrating the distribution of LNAPL in the subsurface.
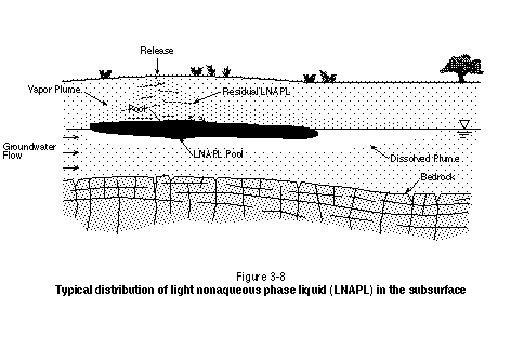
In addition to having pooled LNAPL at positive pressure below the watertable as part of an LNAPL "pancake," watertable fluctuations can bring about smearing of the LNAPL pool below the watertable. As the watertable lowers, the LNAPL pancake will be carried downward. When the watertable rises again, residual LNAPL will be left behind below the watertable. The application of a surfactant or cosolvent flood to remediate LNAPL will need to address both residual and pooled LNAPL present below the watertable. If this LNAPL is not removed, upward diffusion of contaminants and a rising watertable will result in recontamination of the unsaturated zone.
In the case of DNAPL, if the volume of liquid released at ground surface is sufficient, migration will occur down to and below the watertable of an unconfined aquifer. Because DNAPL is typically nonwetting with respect to water, DNAPL migration will tend to take place in coarser-grained materials. DNAPL migrating below the watertable will ultimately come to rest as both residual and pools. DNAPL pools are most likely to form wherever a variation in permeability exists. DNAPL pooled below the watertable exists at positive pressure and will therefore freely enter a borehole or excavation.
At a contaminated site, the spatial distribution of DNAPL migration pathways below the watertable will be governed by geological structure, with migration not necessarily coincident with the direction of groundwater flow. During migration, DNAPL has the potential to pool and flow laterally whenever the capillary pressure at the leading edge of the migrating DNAPL body can no longer overcome the displacement pressure of an encountered lens or lamination. Because displacement pressures are, in general, correlated with hydraulic conductivity, there is the potential for lateral flow and pooling of DNAPL wherever a variation in hydraulic conductivity exists.
The field experiments conducted by Kueper, et al. (1993) demonstrated that even subtle variations in hydraulic conductivity at the centimeter scale can govern the locations of residual and pooled DNAPL. In general, the migration pathways of DNAPL at a contaminated site will be very tortuous and sparsely distributed. Because even subtle variations in geologic structure at the centimeter scale can influence DNAPL migration, it will generally be impossible to locate all individual DNAPL pools and residual zones at contaminated sites using present-day hydrogeological investigation techniques. This statement also applies to the use of partitioning tracers, which is discussed further in Section 5.2.1. Even at sites where an obvious DNAPL trap exists, such as an extensive clay aquitard, there may be many other pools and residual zones at other elevations. Figure 3-9 presents a general schematic illustrating the distribution of DNAPL in the subsurface.
Once NAPL has distributed itself as residual and pools below the watertable, groundwater will flow through these zones, giving rise to evolving dissolved-phase plumes. These plumes will continue to develop until all residual and pooled NAPL has been completely dissolved or the leading edge of the plume is at steady-state with natural attenuation processes. Because groundwater has a higher relative permeability in a residual zone than in a pool, residual NAPL will dissolve more quickly than pooled NAPL. The time required to completely dissolve away either residual or pooled NAPL depends on several factors, including groundwater velocity, the component composition of the NAPL, and the porous media structure.
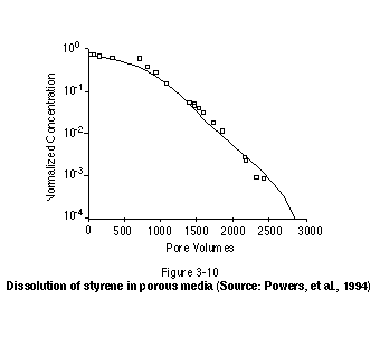
Recent laboratory experiments involving single-component NAPLs have demonstrated that solubility conditions are not maintained in groundwater immediately downstream of a residual or pool zone as it dissolves. Rather, long tailing occurs following a relatively short period of time during which concentrations are near solubility. Figure 3-10, for example, illustrates data collected by Powers, et al. (1994) on the dissolution of NAPL residual in one-dimensional sand columns. After NAPL (styrene) was introduced to the column as residual, the column was flushed with clean water and the concentration of styrene in the effluent was measured. The horizontal axis in Figure 3-10 represents the amount of water flushed through the column in pore volumes. The figure clearly shows that styrene saturation is maintained for only a few tens of pore volumes, after which a long tail is observed. The tailing is in part the result of a reduced NAPL-water interfacial area as the NAPL dissolves and diffusion-controlled dissolution of NAPL situated in pores and pore throats inaccessible to the flowing groundwater. The same tailing phenomenon has been found to occur for the dissolution of NAPL in the presence of surfactants and cosolvents (Abriola, et al. 1993; Mason and Kueper, 1996). In these systems, the degree of tailing observed is generally less for lower groundwater velocities.
At contaminated sites, groundwater will not always flow through residual and pool zones in as ideal a manner as in laboratory experiments. In natural deposits, a heterogeneous distribution of hydraulic conductivity will cause groundwater to flow preferentially through coarser- grained lenses and laminations, resulting in less than optimal contact with certain residual and pool zones. In other words, in addition to diffusion-limited mass transfer at the grain scale, an analogous diffusion-controlled mass transfer may occur at the macroscopic scale, again producing long tailing. Regardless of how important this effect may be, it is clear that even in cases where optimal contact with flowing groundwater occurs, the life span of residual NAPL can be on the order of several decades to centuries depending on the solubility of the particular NAPL components and the magnitude of groundwater velocity.
In addition to hydrodynamic influences such as advection and dispersion, the concentration of a particular contaminant in groundwater downstream of either residual or pooled NAPL will be a function of the component composition of the NAPL. For structurally similar compounds, it has been found that the maximum concentration of a given component in groundwater in contact with NAPL will be proportional to the mole fraction of the component in the NAPL phase (Mackay, et al., 1993; Banerjee, 1984). This is a statement of Raoult's Law, which stipulates that the effective solubility of the component in question will equal the product of its single-component solubility and its mole fraction in the NAPL phase. For a NAPL comprised of ten components in equal mole fractions where each has the identical single-component solubility, for example, the maximum concentration in groundwater for any given component in contact with the NAPL would be 10 percent of its single-component solubility.
For most contaminated sites, the various components comprising the NAPL will not have the same single-component solubilities. In such cases, the more soluble components will preferentially dissolve out of the NAPL relatively quickly, leaving behind the less soluble components to dissolve more slowly. Monitoring wells located downstream of such sources would show declining concentrations over time of the more soluble components, with perhaps relatively unchanging or slightly increasing concentrations over time for the less soluble components. If multicomponent dissolution is not considered when interpreting contaminant concentrations from such a site, the overall low concentrations of all components and the decline in concentration over time of certain components may be taken as a false sign that NAPL is not present in the subsurface.
While multicomponent dissolution can explain some of the temporal variations in contaminant concentration observed at sites, spatial variations occur as well. At sites where the distribution of hydraulic conductivity is highly variable, it follows that residual and pool zones will be distributed in a complex and sparse manner. Because these zones act as sources for dissolved-phase plumes, it follows that such sites will not contain one large, smoothly varying contaminant plume. Instead, the sites will appear to have several isolated plumes, which in two-dimensional cross section do not appear to be related. While these plumes may actually be connected in three dimensions, it is not surprising to find concentration reversals with depth in any given vertical cross section and even monitoring wells exhibiting nondetectable levels of contamination surrounded by wells showing high levels of contamination both above and below. Spatial and temporal variations in plume chemistry also can arise because of variability in processes such as biodegradation and sorption.
Once initial entry into a fracture network has taken place, DNAPL will preferentially migrate through the larger aperture fractures, entering intersecting fractures only if the local capillary pressure exceeds the entry pressure of the newly encountered fracture. The overall pattern of DNAPL migration will be governed by both fluid and media properties. One fluid parameter that has a dramatic influence on the overall migration pathways of DNAPL is interfacial tension. A low interfacial tension will promote migration through a large number of individual fractures because fracture entry pressures will be low. This results in little lateral spreading through the fracture system and large ultimate depths of migration.
A high-interfacial-tension DNAPL, on the other hand, will lead to a smaller number of fractures in the fracture network being invaded by DNAPL. In addition, substantial lateral flow can take place above less permeable rock units because high capillary pressures are required for penetration. Even if lower-permeability rock units become penetrated, lateral flow will continue above because the relative permeability to DNAPL will be higher in the overlying, more fractured, unit. Large amounts of lateral spreading can occur through major bedding partings. Because DNAPL-water interfacial tension largely dictates what the ultimate lateral and vertical extent of DNAPL migration will be in a fracture network, care should be taken to measure this value whenever a sample of DNAPL can be obtained.
Fracture connectivity, spacing, and orientation also have a pronounced influence on DNAPL migration pathways through fracture networks. As in porous media, DNAPL migration will be largely structure controlled. DNAPL will migrate through pathways offering the least capillary resistance, not necessarily coincident with groundwater flow. Hydraulic gradients in most natural groundwater systems are typically very low, having little influence on the direction of DNAPL migration through fractures. A comprehensive monitoring program in fractured media should therefore focus on placing boreholes according to structure, not necessarily according to the direction of groundwater flow.
It should be noted that this discussion assumes that DNAPL migration is limited to the open fractures in a clay or rock deposit. Because the pore openings in a rock or clay matrix are generally very small, an extremely high capillary pressure would be needed to overcome the matrix displacement pressure. Therefore, it is uncommon to find NAPL actually within the matrix of a clay or rock deposit. Exceptions to this include systems where the matrix is wetting with respect to NAPL. The migration of NAPL in fractured rock and clay is discussed in more detail by Kueper and McWhorter (1991); Kueper, et al. (1992); and Pankow and Cherry (1996).
Once NAPL is present in fractured clay or rock in the form of residual and pools, dissolution into flowing groundwater will occur, giving rise to aqueous-phase plumes. Dissolution also will occur into the matrix as a result of molecular diffusion, resulting in contaminants being "stored" in the aqueous phase and sorbed to solid particles. The rate of dissolution of NAPL into the matrix of fractured rock is dependent upon a variety of factors, primarily the aqueous solubility of the NAPL and the porosity of the matrix. For a highly soluble NAPL and/or a moderate to high matrix porosity, the rate of dissolution can be high.
If the matrix has the capacity to store more contaminant mass than is present in the fractures in the form of residual and pooled NAPL, the NAPL will eventually completely deplete itself as a result of molecular diffusion. The advantage of this situation is that it may be possible to drill through fractured rock and clay without risking vertical mobilization of DNAPL because the contaminant is no longer present as an immiscible phase. The disadvantage is that an extremely long time period will be required to remediate the fractured rock or clay environment because of reverse diffusion of contaminants from the matrix back to the open fractures. The matrix can store mass both in the aqueous form and sorbed to solid particles. A higher matrix porosity will allow larger amounts of aqueous phase storage, while higher organic carbon content will result in larger amounts of sorbed storage. Parker, et al. (1994) and Pankow and Cherry (1996) present mathematical solutions to estimate the lifespan of DNAPL in fractured porous media for a variety of source configurations.
It is clear that the application of a surfactant or cosolvent flood is of interest only in cases where residual and pooled DNAPL still exist in fractures. It should also be noted that the increase in contaminant solubility that occurs as a result of surfactant/cosolvent flushing will increase concentration gradients into the matrix, possibly driving more contamination into the matrix. Therefore, surfactant and cosolvent flushing may not be suitable technologies for application in fractured clay or rock where significant matrix porosity exists.
With respect to DNAPL dissolution into flowing groundwater in fractured rock or clay, the same general principles apply as for porous media (effective solubility for multicomponent NAPLs and rate-limited mass transfer). One additional important consideration with respect to the evolution of the dissolved plume, however, is the influence of matrix diffusion. Contaminants in groundwater flowing through the fracture network will diffuse into a porous matrix. The same process applies to the migration of surfactants and cosolvents through fractured media. The effect of matrix diffusion is to slow the rate of solute migration relative to that of groundwater. In other words, matrix diffusion acts as a retardation mechanism in fractured rock. The advantage of this is that contaminants will not be migrating as quickly through fractured rock as may be thought by considering groundwater velocity alone. The disadvantage is that pump-and-treat methods designed to remove aqueous plumes from fractured rock will need to operate for extremely long periods of time because the mass removal process will be limited by the rate of diffusion of contaminants back out of the matrix into the open fractures where groundwater is flowing.
